Tipp 1: Hogyan lehet megtalálni a függvény színátmenetét?
Tipp 1: Hogyan lehet megtalálni a függvény színátmenetét?
gradiens funkciók Vektor mennyisége, amelynek meghatározása összefüggésben van a függvény részleges származékainak meghatározásával. A gradiens iránya jelzi a funkció legmeredekebb növekedésének az útvonalát a skaláris mező egyik pontjáról a másikra.

oktatás
1
A probléma megoldása egy függvény gradiense eseténA differenciál kalkulus módszereit használják, nevezetesen az első rend részleges származékainak meghatározását három változóban. Itt feltételezzük, hogy maga a függvény és valamennyi részleges származéka a folytonosság tulajdonsága a funkció meghatározása területén.
2
A gradiens egy vektor, amelynek irányajelzi az F függvény maximális maximális növekedésének irányát. Ehhez két grafikonon M0 és M1 pontot választanak ki, amelyek a vektor végei. A gradiens nagysága megegyezik az M0-tól az M1 pontig terjedő függvény növekedési sebességével.
3
A funkció minden szempontból differenciálhatóvektor tehát a részleges származékai a koordinátatengelyek vektorának előrejelzései. A gradiens képlet így néz ki: grad = (∂F / ∂x) • i + (∂F / ∂y) • j + (∂F / ∂z) • k, ahol i, j, k az egységvektor koordinátái. Más szóval, egy függvény gradiense egy olyan vektor, amelynek koordinátái részleges derivált gradusai F = (∂F / ∂x, ∂F / ∂y, ∂F / ∂z).
4
Példa 1. Adjuk meg az F = sin (x • z²) / y függvényt. Meg kell találnia a gradiensét a ponton (π / 6, 1/4, 1).
5
Reshenie.Opredelite részleges származékok minden egyes változó esetében: F'_h = 1 / y • cos (x • ZZ) • ZZ; F'_y = sin (x • ZZ) • (-1) • 1 / (y²); F ' _z = 1 / y • cos (x ZZ •) • • 2 x • z.
6
Helyezze a pont koordinátáinak ismert értékeit: F'_x = 4 • cos (π / 6) = 2 • √3; F'_y = sin (π / 6) • (-1) • 16 = -8; F'_z = 4 • cos (π / 6) • 2 • π / 6 = 2 • π / √3.
7
Alkalmazzuk a függvény gradiensének képletét: gr = F · 2 • √3 • i - 8 • j + 2 • π / √3 • k.
8
2. példa. Keresse meg az F = y • arсtg (z / x) függvény koordinátáit az (1, 2, 1) pontban.
9
A megoldás.F'_h = 0 • arstg (z / x) + y • (arstg (z / x)) „_ x = y • 1 / (1 + (Z / X) ²) • (-z / h²) = -y • z / (h² • (1 + (Z / X) ²)) = -1; F'_y = 1 • arstg (z / x) = arstg 1 = π / 4; F'_z = 0 • arstg (z / x) + y • (arstg (z / x)) „_ z = y • 1 / (1 + (Z / X) ²) • 1 / x = y / (x • (1 + (Z / X) ² )) = 1.grad = (-1, tc / 4, 1).
2. tipp: Hogyan találjuk meg a skaláris mező gradiensét?
A skaláris mező gradiense vektor mennyisége. Ezért, hogy megtaláljuk, meg kell határoznunk a megfelelő vektor összes összetevőjét, a skaláris mező eloszlásának ismeretében.
oktatás
1
Olvassa el a magasabb matematika tankönyvében, hogya skaláris mező gradiense. Mint ismeretes, ez a vektormennyiségnek a skaláris függvény maximális csökkenési sebességével jellemezhető iránya van. Az adott vektormennyiség ezen érzését a komponensek meghatározására szolgáló kifejezés indokolja.
2
Ne feledje, hogy a vektort a mennyiségek határozzák megkomponensét. A vektor komponensei valójában ennek a vektornak az előrejelzései egy vagy másik koordináta tengelyre. Így ha háromdimenziós tér van, akkor a vektornak három összetevője kell legyen.
3
Írja le, hogyan határozzák meg a vektor összetevői,amely egy bizonyos mező gradiense. Az ilyen vektor mindegyik koordinátája megegyezik a skaláris potenciál származékával egy olyan változó vonatkozásában, amelynek a koordinátája kiszámításra kerül. Vagyis, ha szükséges a térségi gradiensvektor "Ix" komponensének kiszámításához, akkor meg kell különböztetni a skaláris függvényt az "x" változónál. Vegye figyelembe, hogy a származéknak privátnak kell lennie. Ez azt jelenti, hogy a megkülönböztetés során a fennmaradó változókat, amelyek nem vesznek részt benne, állandónak kell tekinteni.
4
Írjon kifejezést a skalár mezőre. Mint önök is tudják, ez a kifejezés csak többváltozós skaláris függvényt jelent, amely szintén skaláris mennyiségek. A skaláris függvény változóinak számát a tér dimenziója korlátozza.
5
A külön-külön skaláris funkciót differenciáljaminden változót. Ennek eredményeképpen három új funkció lesz. Írja le minden egyes funkciót a skaláris mező gradiensvektorának kifejezésére. A kapott funkciók mindegyike valójában egy adott koordináta egység vektorának együtthatója. Így a végső gradiensvektornak olyan polinomnak kell kinéznie, amelynek együtthatója derivált függvények formájában.
3. tipp: Hogyan találjuk meg a gradienset?
Ha gradiens fogalmát veszi figyelembe, akkor a funkciókat általában skaláris mezőkként értelmezik. Ezért szükséges a megfelelő jelölés bevezetése.

Szüksége lesz rá
- - Boom;
- - a fogantyú.
oktatás
1
Legyen a függvény kap három érv u = f (x,y, z). Egy függvény részleges származtatása, például az x-re vonatkoztatva, az érvre vonatkoztatva származtatott, a fennmaradó érvekkel kapott. A többi érv hasonló. A részleges származék megnevezése a következő formában van írva: df / dx = u'x ...
2
A teljes differenciál egyenlő lesz a du = (df / dx) dx + értékkel(df / dy) dy + (df / dz) dz A részleges származékok a koordináta tengelyek irányában származékként értendők. Ezért felmerül a kérdés, hogy megtaláljuk a származékot az adott vektor s irányára vonatkoztatva az M (x, y, z) pontban (ne felejtsük el, hogy az s iránya meghatározza az s ^ o vektoregység vektort). Ebben az esetben a {dx, dy, dz} = {dscos (alfa), dsos (béta), dsos (gamma)} argumentumok vektorkülönbsége.
3
Figyelembe véve a teljes differenciálforma formáját,következtetni, hogy a származék az irányt-niju s pontjában M egyenlő: (du / dS) | M = ((df / dx) | M) cos (alfa) + ((DF / dy) | M) cos (béta) Ha az s = s (sx, sy, sz), akkor a cos cos (alfa), cos (béta), cos (gamma)} irányú koszinusokat számoljuk ki (lásd az 1. ábrát). 1a).
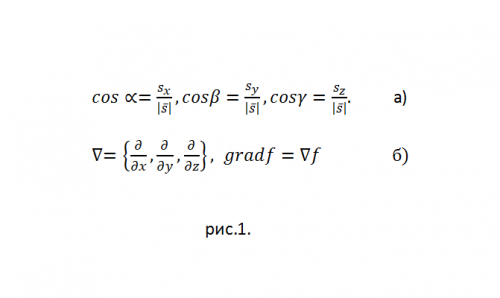
4
Egy származék definíciója egy irányhoz képest, feltételezveM pont a változó lehet újraírni az skalár szorzata: (du / dS) = ({df / dx, df / dy, df / dz}, {cos (alfa), cos (béta) cos (gamma)}) = (grad u, s ^ o). Ez a kifejezés egy skaláris mezőre érvényes. Ha figyelembe vesszük, egy függvény-TION, a gradf - vektor, amelynek koordinátái egybeesik részleges f (x, y, z) .gradf (x, y, z) = {{df / dx, df / dy, df / dz} =) = (df / dx) i + (df / dy) j + (df / dz) k. Itt (i, j, k) a koordináta-tengelyek egységvektorai egy négyszögletes Descartes-koordinátarendszerben.
5
Ha differenciát használszvektor Hamilton-operátor, akkor a gradf ezt a kezelő vektort a skalár f-vel szorozva írja le (lásd az 1b. A kapcsolódás gradf c szempontjából az irányhoz képest az egyenlõség (gradf, s ^ o) = 0 lehetséges, ha ezek a vektorok ortogonálisak. Ezért a gradf gyakran a skaláris mező leggyorsabb változásának iránya. És a differenciálműveletek szempontjából (gradf az egyik), a gradf tulajdonságai pontosan megismételik a funkciók differenciálási tulajdonságait. Különösen, ha f = uv, akkor gradc = (vgradu + u gradv).
4. tipp: Hogyan kell felhívni a gradiens
gradiens Ez egy grafikus szerkesztők számára készült eszköz, amely a vázlat kitöltését az egyik szín egymásra helyezésével végzi. gradiens a kontúrt egy hangerő hatása, szimuláljaa megvilágítás, a tárgy felszínén lévő fény megvilágítása vagy a naplemente hatása a fénykép hátterében. Ezt az eszközt széles körben használják, ezért nagyon fontos, hogy megtanulják használni a fényképeket vagy illusztrációkat.

Szüksége lesz rá
- Számítógép, grafikus szerkesztő Adobe Photoshop, Corel Draw, Paint.Net vagy más.
oktatás
1
Nyisson meg egy képet a programban, vagy hozzon létre egy újat. Hozzon létre egy elérési utat vagy válassza ki a kívánt területet a képen.
2
Kapcsolja be a színátmenet eszközt az eszköztárona grafikus szerkesztõ eszközei. Helyezze az egérmutatót a kijelölt terület vagy vázlat belső pontjára, ahol kezdődik a színátmenet első színezése. Nyomja meg és tartsa lenyomva a bal egérgombot. Vigye a kurzort arra a pontra, ahol a gradiensnek az utolsó színre kell mennie. Engedje el a bal egérgombot. A kiválasztott útvonal kitölti a kitöltést gradienssel.
3
gradiensMegadhatja az áttetszőségt, a színeket és az őketaz arány egy bizonyos beöntési ponton. Ehhez nyissa meg az ablakot a színátmenet módosításához. A szerkesztési ablak megnyitása a Photoshopban - kattintson a "Beállítások" panelen lévő gradiensmintára.
4
A megnyitott ablakban példák formájában megjelenik a színátmenet kitöltésével kapcsolatos lehetőségek. Az egyik lehetőség szerkesztéséhez válassza ki az egérrel.
5
Az ablak alján egy minta jelenik meggradiens egy széles skálán, amelyen a csúszkák találhatók. Csúszkák jelölik pontok, amelyeknél a gradiens kell előre meghatározott jellemzőkkel, és azok között a csúszkákat színe egyenletesen mozog egy előre meghatározott pont az első szín a második pont.
6
A tetején található csúszkákA skálák beállítják a gradiens átlátszóságát. Az áttetszőség megváltoztatásához kattintson a kívánt csúszkára. A skála alatt egy mező jelenik meg, amelyben megadja a kívánt átlátszóság mértékét százalékban.
7
A skála alján található csúszkák megadják a gradiens színeket. Ha rákattint az egyikre, kiválaszthatja a kívánt színt.
8
gradiens több átmenet színe lehet. Más szín megadása - kattintson a mérleg alján található szabad területre. Lesz még egy csúszka rajta. Adja meg a kívánt színt. A skála egy gradiens mintát mutat még egy ponttal. A csúszkákat úgy mozgathatja, hogy a bal egérgombbal tartja őket a kívánt kombináció eléréséhez.
9
gradiensSzámos típus adhatalakú lapos kontúrok. Például egy gömb alakú kör alakításához radiális gradienset használunk, és kúpos alakúak, kúposak. Annak érdekében, hogy a felületet a konvexitás illúziója adja, használhatja a tükör-gradienseket, és gyémánt alakú gradiens használható a kiemelkedések létrehozásához.