LovesTheTeam.com

oktatás

1

A kérdés megválaszolásához a véletlenszerűa normális érték értéke, akkor vonjuk le az entrópia H (x) fogalmát, ami az információelméletben merül fel. Az a kérdés, hogy bármely n-szimbólumból álló diszkrét üzenet, amely X = {x1, x2, ... xn}, diszkrét véletlen változóként értelmezhető egy sor valószínűséggel. Ha a szimbólum használatának valószínűsége például az x5 egyenlő P5-vel, akkor az X = x та esemény valószínűsége azonos. Az információelmélet feltételeitől fogva vesszük az információ mennyiségét (pontosabban a saját információinkat) I (xi) = ℓog (1 / P (xi)) = - ℓogP (xi). A rövidséghez írj P (xi) = Pi-t. A logaritmusok itt a 2. alapon kerülnek meghatározásra. Ezért egyébként egy bináris számjegy (bináris számjegy) egy kicsit.

2

Az entrópia az átlagos számaz információt egyetlen értéke a valószínűségi változó H (x) = M [-ℓogPi] = - ΣPi ∙ ℓogPi (összegzési felett i vedetcya 1-től n). És folyamatos eloszlásokkal rendelkezik. Egy folyamatos, véletlen változó entrópiájának kiszámításához elképzelni azt diszkrét formában. Osszuk az értéktartomány részeit kis időközökkel Δx (kvantálási lépés). Mint lehetséges értéket, vegye a megfelelő Δx közepét, és valószínűsége helyett használja a Pi≈w (xi) Δx területi elemet. A helyzetet az 1. ábra szemlélteti. 1. A kis részletekre mutat egy Gauss görbét, amely a normál eloszlás valószínűségi sűrűségének grafikus ábrázolása. Itt a képlet az adott eloszlás valószínűségi sűrűségére vonatkozik. Óvatosan vegye figyelembe ezt a görbét, hasonlítsa össze az adatokat. Talán a kérdésre adott válasz már feloldódott? Ha nem, érdemes folytatni.

3

Használja az előzőekben javasolt módszertlépés. Számos valószínűséggel hajtson végre egy most diszkrét véletlen változót. Keresse meg az entrópiáját, és adja át a folyamatos eloszláshoz, mivel n → ∞ (Δx → 0). Az összes számítást az 1. ábra mutatja. 2.

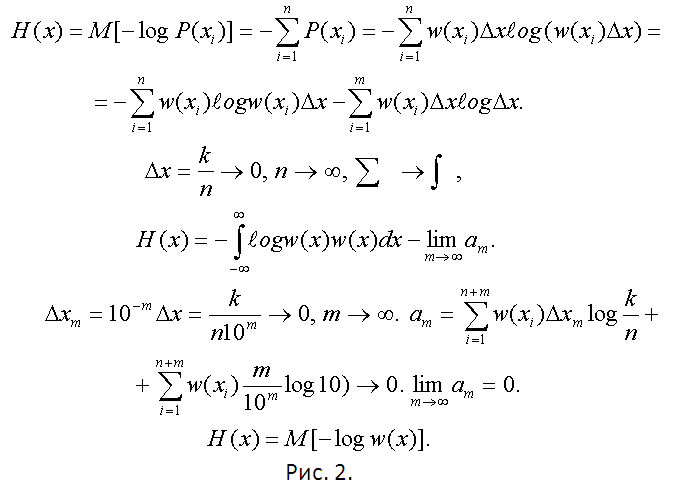
4

Meg lehet bizonyítani, hogy a normál (Gauss)az eloszlások maximális entrópiával rendelkeznek a többiekhez képest. Egy egyszerű számítás a végleges formula az előző lépésben H (x) = M [-ℓogw (x)], hogy ezt az entrópia. Nincs szükség integrációra. A matematikai várakozás tulajdonságai elégségesek. Receive H (x) = ℓog₂ (σh√ (2πe)) = ℓog₂ (σh) + ℓog₂ (√ (2πe)) ≈ℓog₂ (Sx) 2045. Ez a lehető legnagyobb. Most, bármilyen adat áll rendelkezésre az elosztó (kezdve az egyszerű statisztikai összesített), hogy megtalálja a megfelelő variancia Dx = (Sx) ². Behelyettesítve a számított Sx a kifejezés a maximum entrópia. Számítsuk ki a entrópia valószínűségi változó akkor vizsgált H (x).

5

Töltsük fel a H (x) / Hmax (x) = ε arányt. Függetlenül válassza ki az ε0 valószínűségét, amely közel azonos az egységhez, amikor eldönti a terjesztés közelsége és a normális értékeket. Hívja, mondjuk, valószínűtlen valószínűség. A 0,95-nél nagyobb értékek ajánlottak. Ha kiderült, hogy ε> ε0, akkor (valószínűséggel legalább ε0) foglalkozik a Gauss eloszlással.